Convolutional Neural Networks

A Convolutional Neural Network (CNN) is a specific type of feed-forward deep network. CNNs are inspired by the visual cortex of the brain. Some of the individual neurons of the visual cortex are activated only when edges of a particular orientation (e.g. vertical, horizontal) are viewed. These neurons are ordered together in a column and combine together to produce visual perception. Essentially, it is the idea that individual components of a system are specialized for specific tasks.

A CNN has three types of layers: convolutional layers, activation (relu) layers, and pooling layers. In Keras, the convolution and activation layers can be added at the same time. CNNs are typically used for images.

Here is a typical CNN model architecture:

Convolutional Layer

The convolutional layer is the part of the CNN that does the 'heavy lifting'. It consists of a series of learnable filters (kernels). Each filter is set to a certain small size (e.g. 3x3 for a 2D BW image, or 1x3 for a 1D vector). During the pass through the layer, the filter is slid (convolved) across the width and height of the input. As the filter is slid, an activation or feature map is produced that gives the response of the filter at every spatial position. The network will learn filters that activate when they see a specific feature, such as edges if the input is an image. Each convolutional layer has multiple filters and each filter produces a separate activation or feature map. These activation maps are stacked together and passed to the next layer.

For example, consider a 5 by 5 image (green) which only has values 0 or 1 and a 3 by 3 filter (yellow):

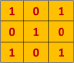
filter

The convolution of the filter across the image would look like this:

The filter is slid across the image by 1 pixel. At every position, the filter is first multiplied elementwise with the pixels of the image and then the resulting values are summed up to get a final integer which is then a single element of the output matrix (feature map). Different values in the filter will create a different output feature map. Here is the keras documentation for convolutional layers

Here is a helpful graphic that shows the result of two different filters being convolved across an image:

An important difference between CNNs and MLPs (Dense layers): An MLP/Dense/Fully connected layer learns global patterns in the input feature space, wheras a CNN/convolutional layer learns local patterns. If we were examining images, a Dense layer would learn patterns that involve all pixels of the image, while a convolutional layer would learn patterns within small windows of the image.

In Keras, a convolutional layer is added by using a Conv1D (for 1D convolutions) or Conv2D (for 2D convolutions) layer:

keras.layers.Conv1D(filters, kernel_size, strides=1, padding='valid', data_format='channels_last', dilation_rate=1, activation=None, use_bias=True, kernel_initializer='glorot_uniform', bias_initializer='zeros', kernel_regularizer=None, bias_regularizer=None, activity_regularizer=None, kernel_constraint=None, bias_constraint=None)

keras.layers.Conv2D(filters, kernel_size, strides=(1, 1), padding='valid', data_format=None, dilation_rate=(1, 1), activation=None, use_bias=True, kernel_initializer='glorot_uniform', bias_initializer='zeros', kernel_regularizer=None, bias_regularizer=None, activity_regularizer=None, kernel_constraint=None, bias_constraint=None)

The arguments we care about for these layers are:

filters - the number of filters used in the layer
kernel_size - the size of the filters
strides - typically = 1, maybe 2, the number of 'pixels'/'elements' the filter shifts over when convolving the image
padding - the amount of empty zero padding around the image, sometimes it is helpful to border the image with 0s, default is no padding
activation - we can combine the conv layer and relu layer in one step by setting this equal to 'relu'

ReLU Layer

A ReLU layer is typically used after every convolution layer. In keras it can be added by setting the activation argument to 'relu'. ReLU stands for rectified linear unit and it is a non-linear operation defined by max(zero, input). Essentially it sets all negative 'pixels'/'elements' of the activation/feature maps to 0. Its purpose is to introduce non-linearity into the data, as real life data is likely to be non-linear. The convolution process is linear, so the ReLU function helps account for the non-linearity.

This image may help visualize what the ReLU step is doing:

Other activation functions can be used besides ReLU, but ReLU has been found to typically perform the best.

Pooling Layer

The function of a pooling layer is to do dimensionality reduction on the convolution layer output. This helps reduce the amount of computation necessary, as well as prevent overfitting. It is common to insert a pooling layer after several convolutional layers.

Two types of pooling layers are Max and Average. Max pooling will take the largest number in a defined spatial neighborhood. Average pooling will take the average value of the spatial neighborhood. Max pooling is the type of pooling typically used, as it has been found to perform better.

There are also Global versions of both of these types of pooling. Global (average or max) pooling is a more extreme method of dimensionality reduction, it averages the input into one value per feature map. A Global pooling layer is often added towards the end of a model, right before the Dense output layer. Here is the keras documentation on Pooling layers.

Here's an example of how the Max and Sum (another type of pooling) layers look:

In Keras pooling layers are added with the following functions:

keras.layers.MaxPooling1D(pool_size=2, strides=None, padding='valid')
keras.layers.MaxPooling2D(pool_size=(2, 2), strides=None, padding='valid', data_format=None)
keras.layers.AveragePooling1D(pool_size=2, strides=None, padding='valid')
keras.layers.AveragePooling2D(pool_size=(2, 2), strides=None, padding='valid', data_format=None)

Global Pooling layers:

keras.layers.GlobalMaxPooling1D()
keras.layers.GlobalAveragePooling1D()
keras.layers.GlobalMaxPooling2D(data_format=None)
keras.layers.GlobalAveragePooling2D(data_format=None)

The argument we care about is:

pool_size - size of the window to 'summarize'

Note that the Global pooling layers do not have any input arguments (except data_format for the 2D ones).

Please see the Keras documentation for arguments not covered here.

Now we will cover an example provided by the Keras documentation for the creation of a 1D CNN. The example can be found here.

1D Convolution example

Here is the code for a complete example of a 1D CNN. We will go through it below.

from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.layers import Embedding
from keras.layers import Conv1D, GlobalAveragePooling1D, MaxPooling1D

seq_length = 64

model = Sequential()
model.add(Conv1D(64, 3, activation='relu', input_shape=(seq_length, 100)))
model.add(Conv1D(64, 3, activation='relu'))
model.add(MaxPooling1D(3))
model.add(Conv1D(128, 3, activation='relu'))
model.add(Conv1D(128, 3, activation='relu'))
model.add(GlobalAveragePooling1D())
model.add(Dropout(0.5))
model.add(Dense(1, activation='sigmoid'))

model.compile(loss='binary_crossentropy',
              optimizer='rmsprop',
              metrics=['accuracy'])

model.fit(x_train, y_train, batch_size=16, epochs=10)
score = model.evaluate(x_test, y_test, batch_size=16)

Import the needed libraries.

from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.layers import Conv1D, GlobalAveragePooling1D, MaxPooling1D

Define the type of model and a variable for the length of the input data. This is an example for 1 dimensional sequence classification so it is referred to as sequence length.
```
seq_length = 64
model = Sequential()
```
Add the first layer. This is a 1D convolutional layer. This layer is using 64 filters (kernels) and a kernel size of 3. We set the activation function we want to apply after the convolution to 'relu' - this defines the ReLU layer. Because it is the first layer we have to define the input shape of the data, this can be a little tricky. The 1D conv function was designed to work with sequential data, so the order of the values can be confusing. The first number represents the number of 'time steps' you have, in this case 64. The second number represents the number of features you have measures for for each time step, in this case 100. When you have a single vector of data per input (e.g. an LB spectrum with 50 eigenvalues), you likely want the last value to be 1 (ex. shape would be (50, 1)).
```
model.add(Conv1D(64, 3, activation='relu', input_shape=(seq_length, 100)))
```
Add another 1D convolutional layer with 64 filters and a kernal size of 3. Add a Relu activation layer after it.
```
model.add(Conv1D(64, 3, activation='relu'))
```
Add a Max pooling layer with a 'window' of size 3 to do dimensionality reduction
```
model.add(MaxPooling1D(3))
```
Add another 2 1D convolutional layers, both with 128 filters and both with ReLU activation layers after.
```
model.add(Conv1D(128, 3, activation='relu'))
model.add(Conv1D(128, 3, activation='relu'))
```
Add a Global average pooling layer to do more dimensionality reduction.
```
model.add(GlobalAveragePooling1D())
```
Add a dropout layer to prevent overfitting.
```
model.add(Dropout(0.5))
```
Add the output layer. This layer is a Dense (fully connected) layer. It only has 1 node as this is a binary classification model. The activation function used is sigmoid. Sigmoid is the most appropriate function to use for a binary classification problem because it forces the output to be between 0 and 1, making it easy to set a threshold (i.e. .5) for classification.
```
model.add(Dense(1, activation='sigmoid'))
```
Compile the model. Because this is a binary classification model we use the loss function 'binary_crossentropy'. The optimizer chosen is 'rmsprop' and we want it to output the accuracy metric.
```
model.compile(loss='binary_crossentropy',
      optimizer='rmsprop',
      metrics=['accuracy'])
      
```
Fit the model. This is what actually trains the model. We give it the input (training data) x_train and y_train. We ask it to run the training 10 times (epoch) and use a batch size of 16. This means it will see 16 inputs before updating the weights.
```
model.fit(x_train, y_train, batch_size=16, epochs=10)
```
Last step is to check the accuracy of the model on some testing data that was kept out of training.
```
score = model.evaluate(x_test, y_test, batch_size=16)
```

That's it! You now know the basics of a CNN in Keras. A 2D CNN, such as for pictures, can have the same format. You would just use the 2D version of the functions and adjust the kernal size to be two dimensions etc.

Please continue on to Activation Functions.